Flugvorbereitung

 

Obwohl heute realiter keine Flugvorbereitung mehr mit Karte und Lineal gemacht wird, um daraus Strecken und Kurse zu entnehmen, behalte ich diesen Artikel bei. In den Zeiten von komfortablen Flugplanungsprogrammen ist es ja vielleicht für den ein oder Anderen trotzdem interessant zu erfahren, wie solche Programme rechnen.

Alle Flugvorbereitungsprogramme bestimmen zunächst aus den geographischen Koordinaten des Start- und Zielpunktes die zurückzulegende Entfernung und den zugehörigen rechtweisenden Kurs. Dies ist wohl der anspruchsvollste Teil der Rechenarbeit, weil man hierfür auf die sphärische Trigonometrie angewiesen ist. Aus den Windangaben und der Eigengeschwindigkeit kann dann der Luvwinkel und die Grundgeschwindigkeit errechnet werden. Dafür reicht schon die Trigonometrie der Ebene. Für den Rest benötigt man nur noch die Grundrechenarten und einen simplen Dreisatz: Die Ortsmißweisung und die Deviation führen zum Kompaßsteuerkurs, über die Geschwindigkeit und Flugstrecke wird die benötigte Zeit und mit Hilfe des Verbrauchs die benötigte Kraftstoffmenge errechnet.

Insgesamt also eine Aufgabe, die, mit etwas Nachhilfe, von einem Tabellenkalkulationsprogramm erledigt werden kann. Die Nachhilfe bezieht sich darauf, zur Berechnung der benötigten Größen

• Distanz,
• Kurs,
• Luvwinkel und
• Grundgeschwindigkeit

eigene Funktionen zu definieren. Anschließend an die Darstellung der mathematischen Grundlagen zur Bestimmung der jeweiligen Größen werden Realisierungsmöglichkeiten in VBA für EXCEL 97 dargestellt.

Bestimmung der Distanz

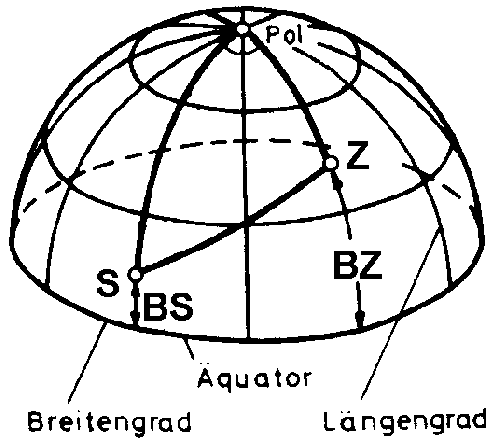
Die Ermittlung der Entfernung aus den geographischen Lagedaten geschieht mit Hilfe der sphärischen Trigonometrie. Ausgangspunkt ist ein Kugeldreieck oder sphärisches Dreieck, bestimmt durch drei Großkreisbögen, die sich nicht in den Endpunkten eines Kugeldurchmessers schneiden. Der größeren von zwei Seiten liegt der größere Winkel gegenüber. Die Seiten a, b und c werden als Winkel im Kugelmittelpunkt gemessen.

Für die Berechnung der Entfernung verwendet man den Seitencosinussatz:

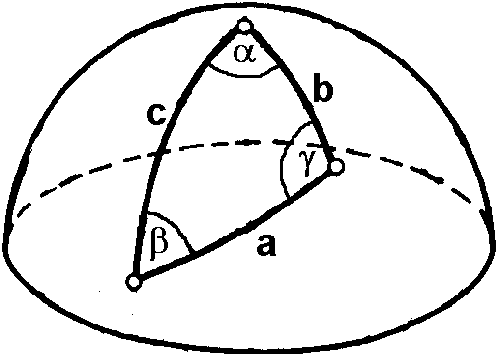
1. cos a = cos b × cos c + sin b × sin c × cos a

Der Startort S ist durch seine Breite (BS) und Länge (LS) und ebenso der Zielort Z durch Breite (BZ) und Länge (LZ) bestimmt. Vom Pol aus werden die beiden Orte durch den Winkel a =D L eingeschlossen, der sich durch die Differenz der Längengrade von Start- und Zielort ergibt.

Nach dem Seitencosinussatz ergibt sich für die Entfernung a zwischen Start und Ziel:

1. cos a = cos (90°–BZ) × cos (90°–BS) + sin (90°–BZ) × sin ( 90°–BS) × cos (dL)

oder kürzer:

1. cos a = sin BZ × sin BS + cos BZ × cos BS × cos (dL)

Berechnet wird der Cosinus des Winkels a, dessen Scheitel im Kugelmittelpunkt liegt, und dessen Schenkel durch S bzw. Z gehen. Um die tatsächliche Entfernung zwischen S und Z auf der Kugeloberfläche zu erhalten, muß der Arcuscosinus gebildet und von der Einheitskugel in die reale Erdkugel umgerechnet werden:

dist = arccos a × Erdradius

Leider steht auf dem PC meist die Arcuscosinus-Funktion nicht zur Verfügung, so daß man in den Arcustangens umrechnen muß:

 mit: , also: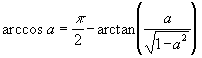 

Function dist(BS, LS, BZ, LZ) Erdradiuskm = 6370 ErdradiusNM = Erdradiuskm * 0.53996  u_bf = Application.Pi() / 180 dL = Abs(LS - LZ)  x = Sin(BS * u_bf) * Sin(BZ * u_bf) + Cos(BS * u_bf)       * Cos(BZ * u_bf) * Cos(dL * u_bf) y = Application.Pi() / 2 - Atn(x / Sqr(1 - x ^ 2)) dist = y * ErdradiusNM End Function

Bestimmung der Distanz Erdradius in km  Erdradius in NM Umrechnungsfaktor Grad in Bogenmaß Längenunterschied zw. Start und Ziel abgeleitete Funktion für ArcCos Funktionsergebnis

 

 

 

 

 

 

 

Bestimmung des Kurses

Im rechtwinkligen Kugeldreieck gilt: 

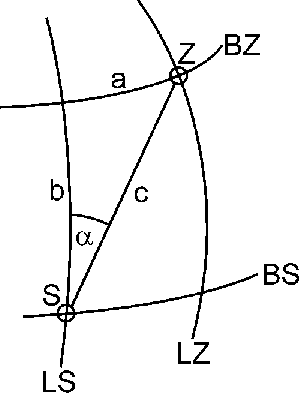
Die Strecke a ist die Längendifferenz zwischen Start- und Zielort im Bogenmaß, wobei auch noch die Abweitung berücksichtigt werden muß; b errechnet sich aus der Breitendifferenz zwischen Start- und Zielort im Bogenmaß. Der Winkel a selbst wird also über den Arcustangens bestimmt.

Function rwk(BS, LS, BZ, LZ) u_bf = Application.Pi() / 180 dL = Abs(LS - LZ) dB = Abs(BS - BZ) If dL = 0 Then If BS > BZ Then K = 180 Else K = 0 End If End If If dB = 0 Then If LS < LZ Then K = 90 Else K = 270 End If End If u_b = dL * u_bf * Cos((BS + BZ) / 2 * u_bf) a = dB * u_bf winkel = Atn(Tan(a) / Sin(u_b)) gradzahl = winkel / u_bf If LS < LZ Then If BS < BZ Then K = 90 – gradzahl Else K = 90 + gradzahl End If Else If BS < BZ Then K = 270 + gradzahl Else 270 – gradzahl End If End If rwk = K End Function

'Kursbestimmung 'Umrechnungsfaktor Grad in Bogenmaß 'Längendifferenz 'Breitendifferenz 'Wenn Längendiff. gleich 0, also N- oder S-Kurs 'Wenn Startbreite > Zielbreite 'dann Südkurs 'sonst 'Wenn Breitendiff. = 0, also O- oder W-Kurs 'Wenn Startlänge < Ziellänge 'dann Ostkurs 'sonst 'Westkurs 'Längendiff. im Bogenmaß (um Abweitung korr.) 'Breitendifferenz im Bogenmaß 'Berechnung des Winkels im Bogenmaß 'Winkel in Grad 'Wenn Startlänge < Ziellänge, also Richtung O 'Wenn Startbreite > Zielbreite 'dann Nordostkurs 'sonst 'Südostkurs 'sonst grob Richtung Westen 'Wenn Startbreite < Zielbreite 'dann Nordwestkurs 'sonst 'Südwestkurs 'Funktionsergebnis

Bestimmung des Luvwinkels

Für die Berechnung des Luvwinkels aus dem Kurs, der Eigengeschwindigkeit v_e, der Windgeschwindigkeit W_V und der Windrichtung W_W ist die Trigonometrie der Ebene völlig ausreichend.

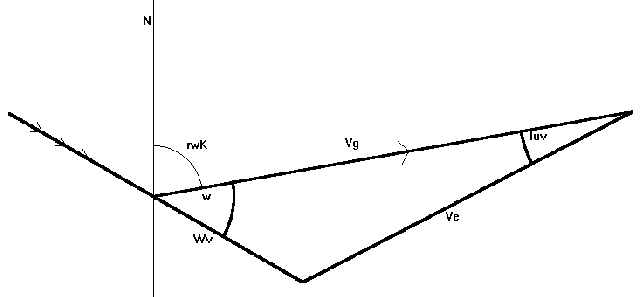
Für die Bestimmung des Luvwinkels müssen der rechtweisende Kurs (rwK), die Eigengeschwindigkeit (v_e) sowie der Wind nach Richtung und Stärke bekannt sein. Im Winddreieck tritt der Luvwinkel zwischen den Schenkeln v_g und v_e auf. Er kann mit dem Sinussatz

berechnet werden, wenn die dem Winkel gegenüberliegende Seite (i.e. die Windgeschwindigkeit) und ein weiteres Paar aus Winkel und gegenüberliegender Seite bekannt sind. Im konkreten Fall bietet sich die Kombination aus dem Schenkel v_e und dem Winkel w zwischen dem Windvektor und dem rwK an. Dieser Winkel w errechnet sich aus der Differenz zwischen der Windrichtung± 180° und dem rwK. Allerdings muß man bei dieser Differenzbildung überlegt vorgehen, da nicht nur der Differenzbetrag, sondern auch dessen Vorzeichen von Bedeutung ist.

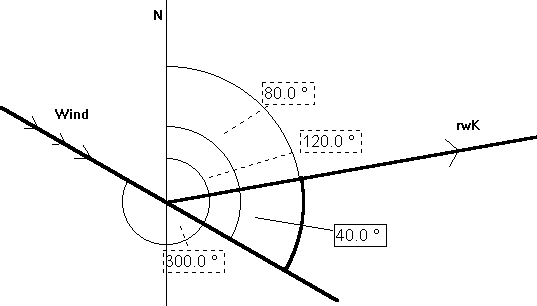
Kommt der Wind von links auf den Kurs, so muß kleiner gesteuert werden, der Luvwinkel bekommt demnach ein negatives Vorzeichen.

Wind von rechts ergibt einen größeren Steuerkurs, also einen Luvwinkel mit positivem Vorzeichen.

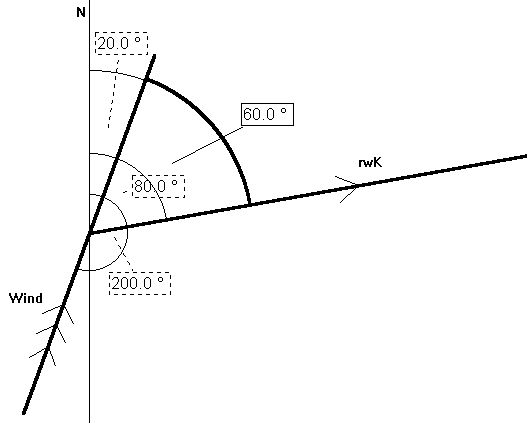
Winkelbeziehung	Wind von ...	Luvwinkel ist ...
(Windrichtung ± 180°) > rwK	links	negativ
(Windrichtung ± 180°) < rwK	rechts	positiv

Es wird klar, dass die Winkeldifferenz ausgehend vom rwK gemessen werden muß. Vom Schenkel v_g misst man im Uhrzeigersinn in mathematisch negativer Richtung, gegen den Uhrzeigersinn ist die mathematisch positive Richtung. Der benötigte Winkel w wird also durch den Term K - (Windrichtung ± 180°) bestimmt.

Nach dem Sinussatz ergibt sich nun:

Function luv(Kurs, Ve, Ww, Wv) u_bf = Application.Pi() / 180 w = (Kurs - Ww - 180) * u_bf x = Sin(w) * Wv / Ve luv = Atn(x / Sqr(1 - x ^ 2)) / u_bf End Function

'Bestimmung des Luvwinkels 'Bestimmung des Winkels zwischen Vg und Ww 'Sinus des Luvwinkels bestimmen 'Berechnung über die VBA-Funktion Arctan

Function luv1(Kurs, Ve, Ww, Wv) u_bf = Application.Pi() / 180 w = (Kurs - Ww - 180) * u_bf sluv = Sin(w) * Wv / Ve luv1 = Application.Asin(sluv) / u_bf End Function

'Bestimmung des Luvwinkels 'Winkel zwischen Vg und Ww 'Sinus des Luvwinkels bestimmen 'Berechnung mit der Arcsin-Funktion von EXCEL

Bestimmung der Grundgeschwindigkeit

Ist der Luvwinkel bekannt, läßt sich die Grundgeschwindigkeit ebenfalls mit dem Sinussatz bestimmen, wobei mit x der Winkel zwischen dem Windschenkel und dem Schenkel v_e bezeichnet wird. Dieser Winkel x wird einfach durch Ergänzung auf 180° bestimmt.

Function Vg(Kurs, Ve, Ww, Wv, luv) u_bf = Application.Pi() / 180 x = (Kurs - Ww - 180 + luv) * u_bf w = (Kurs - Ww - 180) * u_bf Vg = Ve * Sin(x) / Sin(w) End Function

'Bestimmung der Grundgeschwindigkeit 'Winkel zwischen Wv und ve 'Winkel zwischen vg und Wv 'Funktionsergebnis

Es geht auch über den Cosinussatz: c² = a² + b² - 2× a× c× cos g . Bezogen auf unser Winddreieck bedeutet dies:

v_g² = w_v² + v_e² - 2× w_v× v_e× cos x bzw.

Function Vg1(Kurs, Ve, Ww, Wv, luv) u_bf = Application.Pi() / 180 x = (Kurs - Ww - 180 + luv) * u_bf Vg1 = Sqr(Ve * Ve + Wv * Wv + 2 * Ve * Wv * Cos(x)) End Function

'Bestimmung der Grundgeschwindigkeit

Die Bestimmung des Luvwinkels kann natürlich auch in der Funktion selbst geschehen, man integriert dazu einfach die obige Funktion zur Bestimmung des Luvwinkels:

Function Vg2(Kurs, Ve, Ww, Wv) u_bf = Application.Pi() / 180 w = (Kurs - Ww - 180) * u_bf sluv = Sin(w) * Wv / Ve luvw = Atn(sluv / Sqr(1 - sluv ^ 2)) / u_bf x = (Kurs - Ww - 180 + luvw) * u_bf Vg2 = Ve * Sin(x) / Sin(w) End Function

'Bestimmung der Grundgeschwindigkeit 'Bestimmung des Winkels zwischen Vg und Ww 'Sinus des Luvwinkels bestimmen 'Berechnung des Luvwinkels 'Winkel zwischen Wv und ve 'Funktionsergebnis

Realisierung in einer Tabellenkalkulation

Durch ihre Leistungsfähigkeit bieten sich moderne Tabellensysteme ganz besonders zur Bestimmung der benötigten Flugdaten an.

Definieren der Funktionen

Über die Unzahl der eingebauten Funktionen hinaus ermöglichen wohl alle Kalkulationsprogramme die Definition benutzerdefinierter Funktionen. Die konkrete Vorgehensweise wird sich natürlich von Programm zu Programm und innerhalb einer Programmlinie auch von Version zu Version unterscheiden, mit dem Handbuch oder dem Hilfesystem wird man aber schnell die korrekte Vorgehensweise ermitteln können.

Im Falle von EXCEL 97 geht man folgendermaßen vor:

Man beschafft sich eine (neue) Mappe und ruft über Extras/Makro den Visual-Basic-Editor auf. Dort beschafft man sich ein neues Modul (Einfügen/Modul) und ebendort eine neue Prozedur (Einfügen/Prozedur). Im erscheinenden Dialog gibt man den Namen der Funktion an (beispielsweise "dist") und wählt den Typ "Function". Nach dem Klick auf den OK-Knopf wird der Funktionsrumpf erstellt. In die noch leere Klammer nach dem Funktionsnamen in der ersten Zeile tippt man, durch Kommata getrennt, die benötigten Parameter (im gewählten Beispiel: BS, LS, BZ, LZ). Zwischen Funktionskopf und –ende kommen die zugehörigen Anweisungen.

Es empfiehlt sich, die Funktion gleich über das gleichnamige Menü zu "testen", indem man das VBA-Projekt kompilieren läßt. Eventuelle (Schreib-)Fehler werden dann gleich im Funktionstext markiert.

Aufruf der Funktionen

Auf dem EXCEL-Tabellenblatt ist die Funktion dann sogleich einsatzbereit. Sogar der Funktionsassistent hält sie schon unter der Kategorie "Benutzerdefiniert" bereit und fragt korrekt die definierte Anzahl an Parametern ab.

Formular zur Flugvorbereitung

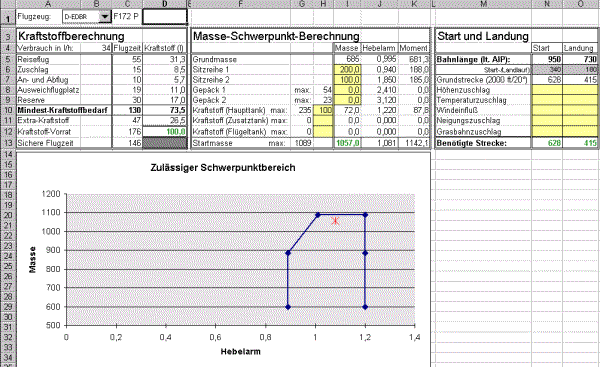
Hat man etwas mit den selbstdefinierten Funktionen "herumgespielt", so erwacht bald der Wunsch nach einem komfortablen Flugplanungsformular. Man möchte beispielsweise nicht immer nach den Koordinaten der Start- und Landeplätze suchen müssen, sondern diese in einer kleinen Datenbank samt weiteren relevanten Angaben (ICAO-Kennung, Frequenz, Bahnlänge, ...) vorhalten und nur aus einer Liste wählen. Nachdem man dann noch meteorologische und flugzeugbezogene Daten eingegeben hat, werden alle Werte ausgerechnet und das Planungsformular wie von Zauberhand gefüllt.

Auch die nötige Spritberechnung, die an anderer Stelle angehandelte Bestimmung des Schwerpunkts und der benötigten Bahnlänge kann eigentlich auch das Programm bestimmen. Aus diesen Überlegungen ist ein Flugplanungsformular in EXCEL entstanden, das diese Punkte automatisch erledigt.

Eine Warnung zum Schluss

Fehler sind menschlich, auch Computer produzieren Fehler: Überprüfen Sie also die erhaltenen Werte kritisch! Für die Folgen einer eventuellen Landung auf dem Roten Platz in Moskau komme ich selbstverständlich nicht auf. Außerdem wäre ein solcher Flug seit Rust auch nicht mehr besonders originell...