Die grundlegenden Elemente und Zusammenhänge der Abbildungsgeometrie lassen sich vorteilhaft mit Hilfe dynamischer Geometrie darstellen und nachvollziehen. Voraussetzung zum Bearbeiten der nachfolgenden Darstellungen ist ein auf dem Rechner installiertes und freigegebenes Java. Nähere Hinweise erhalten Sie am Ende dieser Seite. Am fruchtbarsten und am nachhaltigsten wird Ihr Erkenntnisgewinn sein, wenn Sie die nachfolgenden Applets selbst in Cinderella oder einem anderen geeigneten dynamischen Geometriesystem nachbilden!
Kongruenzabbildungen
Zwei Achsen
Die sicher bekannteste Kongruenzabbildung ist die Geradenspiegelung. Sie ist zugleich die "erzeugende" Kongruenzabbildung, da sich aus ihr alle weiteren Kongruenzabbildungen erzeugen lassen. Wir beginnen mit der Hintereinanderausführung von zwei Geradenspiegelungen an zwei verschiedenen Geraden der Ebene. Für zwei Geraden in der Ebene gibt es (außer der Identität) genau zwei verschiedene Lagebeziehungen: Entweder schneiden sich beide Geraden in einem Punkt oder sie sind zueinander parallel. Erarbeiten Sie mit den beiden folgenden Konstruktionen, welche Kongruenzabbildung durch die Hintereinanderausführung zweier Achsenspiegelungen an sich schneidenden bzw. parallelen Achsen entsteht:
Offensichtlich ergibt die Hintereinanderausführung von zwei Achsenspiegelungen entweder eine Drehung oder eine Verschiebung. Umgekehrt kann jede Drehung bzw. Verschiebung durch die Hintereinanderausführung von zwei Achsenspiegelungen an zwei geeignet plazierten Achsen ersetzt werden. Finden Sie mit den folgenden Konstruktionen heraus, wie die Achsen jeweils plaziert werden müssen, um eine gegebene Drehung bzw. Verschiebung zu ersetzen:
Drei Achsen
Bei der Hintereinanderausführung von drei Geradenspiegelungen unterscheiden wir zunächst zwei Fälle: Entweder liegen die Achsen im Büschel oder sie liegen beliebig in der Ebene. Die Büschellage unterteilen wir in kopunktale und parallele Geraden.
Drei Geraden in allgemeiner Lage
Vier Achsen
Bei der Hintereinandrausführung von vier Achsenspiegelungen entstehen keine weiteren Kongruanzabbildungen mehr, viel mehr lassen sich vier und mehr Achsenspiegelungen immer auf weniger Spiegelungen reduzieren. Im Folgenden werden drei Fälle dargestellt, wir beginnen mit den Sonderfällen:
Vier Geraden: Je zwei Achsen senkrecht aufeinander
Vier Geraden: Je zwei Achsen parallel
Vier Geraden: Je zwei Achsen schneiden sich
Ähnlichkeitsabbildungen
Bekannte Vertreter von Dilatationen sind Verschiebungen und zentrische Streckungen.
Zentrische Streckung
Verknüpfung von Dilatationen
Zentrische Streckung und Verschiebung
Verschiebung und zentrische Streckung
Affine Abbildungen
Affine Abbildung eines Dreiecks
Affine Abbildung eines Vierecks
Projektive Abbildungen
Projektive Abbildung eines Vierecks
Konforme Abbildungen
Spiegelung einer Geraden am Einheitskreis
Spiegelung eines Kreises am Einheitskreis
Voraussetzungen zum Ausführen der obigen Applets
Zum Bearbeiten der obigen Darstellungen muss auf Ihrem Rechner Java installiert und zur Ausführung freigegeben sein! So Sie bereits Cinderella installiert haben, sollte dies der Fall sein.
Da viele Browser Java-Applets aus Sicherheitsgründen sperren, müssen Sie in aller Regel explizite Ausnahmen formulieren, damit Ihr Browser die obigen Inhalte überhaupt darstellt. Solche Ausnahmen formuliert man, indem man die WWW-Seiten angibt, von denen der Browser Java-Applets laden und darstellen darf. In diesem Fall handelt es sich um meine private Homepage http://www.albrecht57.de und die Homepage von cinderella http://cinderella.de. Wo diese Ausnahmen eingetragen werden, hängt leider vom verwendeten Betriebssystem und teilweise vom Browser ab.
Windows
In der Windows-Welt müssen die Ausnahmen direkt im Browser eingetragen werden, indem meist Ausnahmelisten um die angegebenen Internetadressen erweitert werden. Wie dies genau geht, hängt vom jeweiligen Browser ab.
Eine gute Übersicht liefert:
https://java.com/de/download/help/enable_browser.xml
Über diese Seite können Sie Java nötigenfalls auch herunterladen und installieren.
Mac
Auf dem Mac werden die Ausnahmen für Java zentral über die Systemeinstellungen verwaltet. Öffnen Sie daher die Systemeinstellungen und wählen Sie dort das Icon Java:

Sollte das Java-Icon nicht in Ihren Systemeinstellungen erscheinen, dann ist Java noch nicht auf Ihrem Rechner installiert. Sie können es über die oben angegebene Seite von Java beziehen.
Nach dem Klicken erscheint ein Fenster, in welchem mitgeteilt wird, dass das Java Control Panel in einem separaten Fenster geöffnet wird:

Beim ersten Aufruf müssen Sie nichts weiter unternehmen. Falls Sie das Control-Panel bereits aufgerufen hatten, klicken SIe auf den Button: "Java Control Panel erneut öffnen". Nach kurzer Wartezeit erscheint dann das Control-Panel, dort wählen Sie die Registerkarte Sicherheit:
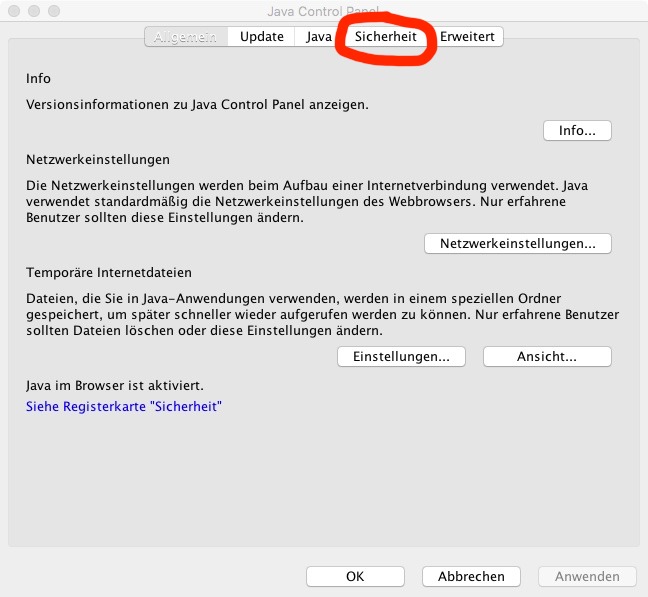
Im Fenster "Sicherheit" achten Sie darauf, dass die Sicherheitsebene nur auf "Hoch" (und nicht auf "Sehr hoch") eingestellt ist und klicken auf "Siteliste bearbeiten":
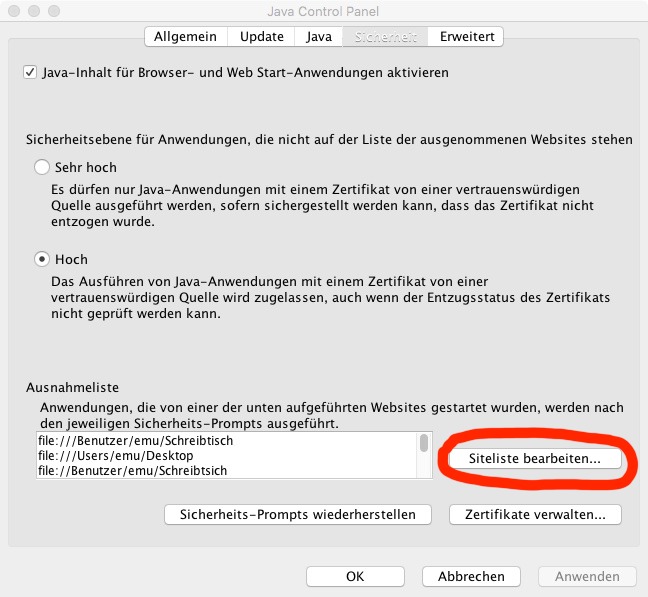
Sie erhalten dann eine Ausnahmeliste, in welcher diejenigen Sites eingetragen sind, die Sie als vertrauenswürdig eingestuft haben und von denen Java-Applets bezogen und zur Ausführung gebracht werden dürfen. Klicken Sie auf "Hinzufügen" und tragen Sie die freizugebenden WWW-Seiten ein. Falls bei Ihnen schon mehrere Einträge vorhanden sind, müssen Sie diese Liste zuvor ganz nach unten scrollen, um eine leere Zeile zu erhalten.
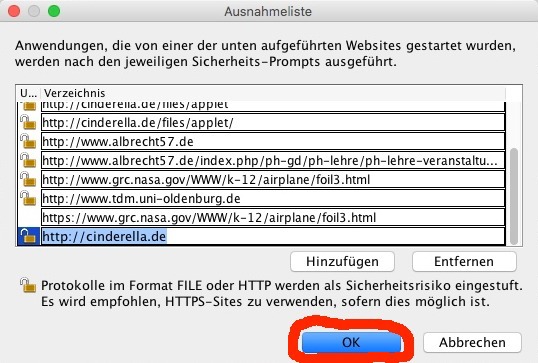
Tragen Sie als neue Seite zunächst
http://cinderella.de
ein und klicken Sie dann auf "OK". Die folgende Warnung übergehen Sie mit "Fortfahren":
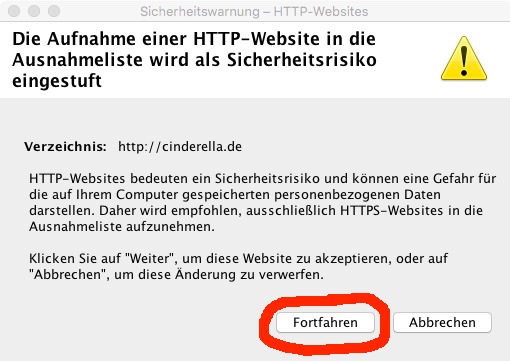
Jetzt kommen Sie wieder auf die Seite "Sicherheit" zurück und führen den Prozess des Hinzufügens einer WWW-Seite in die Ausnahmeliste nochmals durch, indem Sie nun die Adresse
http://www.albrecht57.de
eintragen.
Damit müssten die obigen Java-Applets zur Abbildungsgeometrie auf Ihrem Mac problemlos laufen. Es kann Sein, dass Sie diese Applets mehrfach aufrufen müssen, dass Sie trotzdem noch Sicherheitsanfragen bekommen, ob denn die gewählte Seite wirklich ausgeführt werden soll und es kann sein, dass Sie Ihren Mac neu starten müssen, damit die durchgeführten Veränderungen in Kraft treten.
